Do Ponto de Vista Para a Flutuação
Brunelleschi inventou o dispositivo que simula a geometria da visão no qual Alberti baseou sua teoria da perspectiva, descrita no Tratado da Pintura (1435). Era o Renascimento florescendo e propondo um sistema que necessitava das coisas do mundo “que ocupam um lugar”. Argan (1999, p. 85-89) se refere aos retábulos de Brunelleschi, que teriam sugerido à Alberti o princípio de sua câmara obscura, ressaltando que nestes, o céu é ora o reflexo do próprio céu em uma superfície de prata brunida, ora o próprio céu funcionando como fundo de um recorte no próprio retábulo. Essa opção, nos diz Argan, se explica na medida em que “o céu não ocupa ‘um lugar’, portanto não pode ser reduzido à medida (…)”. Como não pode representar o céu, “ou seja, incluí-lo no sistema proporcional que define a forma, o artista renuncia a pintá-lo”. (Idem, p. 88). Propomos pensar que a representação Ocidental, num arco de tempo que, simplificadamente, vai de Alberti a Cézanne, se alicerça numa certa renúncia a representar aquilo que contém ambiguidade. Sob esse ponto de vista — baseado num espaço Euclidiano — a visão funcionou como operador da representação do espaço, logo mais mediada pelos avanços da geometria descritiva e da matemática, que conduziu a arte em suas mais diversas manifestações até um certo ponto de não retorno nas vanguardas do início do século XX.

A perspectiva a partir da qual pretendemos montar a narrativa que conduz este artigo, define um ponto de desmaterialização do objeto, ou, das coisas do mundo que ocupam “um lugar”, que coincide com um esforço humano em representar uma tal dimensão imaterial, ambígua, que se apresenta inicialmente enquanto curiosidade, e que viria mais tarde a ser amparada pela física no assombro de teorias que vão de Riemann à Einstein e sua teoria da relatividade. Um esforço de caráter abstrato mais amplo manifesta-se simultaneamente, ainda que não coletivamente, com o Suprematismo e o Construtivismo na Rússia, o Futurismo na Itália, o Dadaísmo, finalmente concentrado em Paris, o Neoplasticismo na Holanda e o Concretismo, mais tardio e de certa forma inclusivo, para citarmos apenas ápices de uma história que envolve múltiplas manifestações e que tece um trânsito científico e artístico que envolve protagonistas diversos. É nesse contexto que surgem as genericamente chamadas “axonométricas de Theo van Doesburg”, a partir das quais pretendemos demonstrar uma visão abstrata da perspectiva como ponto chave para uma nova visão da arte e do mundo, calcada no imaginário vigente no início do século XX. E, em que pese à importância de Theo van Doesburg por seu protagonismo no movimento De Stijl, cuja revista de mesmo nome fora lançada em 1917, é sobre suas especulações em torno da representação que este artigo se debruça.

Não basta, no entanto, partirmos de tais dispositivos sem mencionar que o uso da axonometria data da China antiga, de acordo com o panorama histórico esboçado por Yve-Alain Bois (1981)¹. No ocidente, é igualmente importante citar o seu uso no âmbito militar desde o Renascimento, no qual foi chamada de projeção militar. Da mesma forma, a utilização da representação por meio da projeção axonométrica está presente nas escolas de engenharia do final do século XIX, das quais emerge a figura de Auguste Choisy (1841-1909) (BANHAM, 1979; BOIS, 1981) que exerceu, certamente, uma considerável influência no universo da arquitetura e, consequentemente, de alguma forma, na arte do período. No entanto, o que demarca o ponto de partida que interessa a este artigo é a exploração, empreendida por Theo van Doesburg, da axonométrica sob o ponto de vista estético, como apontado por Yve-Alain Bois em seu Metamorphosis of Axonometry² (1981. p. 42), opinião que é retomada por Robin Evans em seu Projective Cast (1995), do qual vale ressaltar a seguinte passagem:

Os pintores com ambições arquitetônicas provocaram uma mudança de sensibilidade ao explorar uma ambiguidade visual que faz com que o espectador se perca. Ao mesmo tempo, eles encontraram uma forma de deformação dimensional nas imagens. As certezas foram trocadas. Os observadores, que conheciam o seu lugar na perspectiva, não estão amarrados na axonometria. É como se estivéssemos flutuando. Van Doesburg aprimorou o efeito removendo todas as indicações de orientação ou fechamento nas contracomposições e também girando 45 graus algumas das folhas em que foram desenhadas. Sugere-se uma semelhança entre o observador flutuante e os planos flutuantes. Se todos flutuarmos, todos flutuaremos em alguma coisa: o espaço, o espaço do século XX, diz Bois. (EVANS, 1995, p. 339. Tradução nossa).

Deliciosamente Flutuando no Espaço
Para Bois, a retomada da axonometria tem, na representação do Proun (1919) de El Lissitzky, sua “certidão de nascimento” (BOIS, 1981. p. 42). Mas o interesse para esta análise recai sobre a produção de axonométricas de Van Doesburg, especialmente entre 1923 e 1924, pois nela é possível encontrar pontos de contato com a matemática e com um imaginário muitas vezes mal compreendido que é explicitamente citado em alguns de seus títulos.

É sabido que Van Doesburg passa a investigar a construção do espaço por meio de axonometrias a partir da exposição “Les architectes du group De Stijl” na galeria parisiense L’Effort Moderne, em 1923, de propriedade de Léonce Rosenberg. É na parceria entre Van Doesburg e, o então estudante de arquitetura, Cornelis van Eesteren, que este apresenta a perspectiva axonométrica a Van Doesburg, quando de seus projetos em conjunto para a Maison Particulière, seguido pelo projeto da Maison D’Artiste (ambos desenvolvidos no verão de 1923, no studio da Rue de Moulin), apresentados na exposição citada, assim como o projeto para o Hôtel Particulière, desenvolvido para Rosenberg (figura 1). Após essa produção inicial, Van Doesburg faz uma série de axonométricas chamadas de Contraconstruções (Counter-constructions) simultaneamente a sua produção pictórica, na qual investiga a curiosa figura do tesserato.

O tesserato é denominado e desenvolvido, teórica e geometricamente, pelo matemático Charles Howard Hinton, que publica, entre outros, dois livros influentes: A New Era of Thought, em 1888, e The fourth dimension, em 1904. A filosofia de Hinton propõe pensarmos em uma dimensão que não percebemos, o que envolve um sentido transcendente, mas, ainda que sua filosofia do hiperespaço tenha sido banhada em uma aura mística, Hinton empreende um esforço bastante abstrato para representar a figura do cubo na quarta dimensão, o tesserato. Essa investigação, na nossa opinião, é levada adiante por Theo van Doesburg, movido por interesses estéticos, imbuídos de aspectos metafísicos, mas não místicos, claros na formulação do Neoplasticismo, ao que procuraremos demonstrar a seguir.

Matemática, Geometria e Misticismo
Aqui é preciso uma breve introdução sobre o percurso da geometria de plano e sólido estruturada por Euclides em Elementos (300a.c.) e sua influência na subjetividade espaçotemporal humana e, por consequência, nas representações que articulam o entendimento e percepção desta acerca do universo até um ponto de não retorno com os desdobramentos de uma nova concepção de espaço multidimensional, moderna, originada “não antes das primeiras décadas do século XIX” (Manning, 1914, p.1). Em Geometry of Four Dimensions (1914), Henry Parker Manning apresenta um panorama de como a concepção de dimensão espacial no Ocidente, desde Aristóteles, esteve imanente ao espaço natural: os gregos concebiam o número como uma linha no espaço, e ao debruçarem-se sobre o que seriam as dimensões, tal concepção e suas ferramentas admitiam não mais que três, atreladas ao espaço natural percebido. Manning cita a justificativa para tal, que se encontra nos comentários do filósofo bizantino Simplício ( 480 d.C.), que escreve:

O admirável Ptolomeu, em seu livro Sobre a Distância, provou bem que não existem mais do que três distâncias, devido à necessidade de que as distâncias sejam definidas e que as distâncias definidas sejam tomadas ao longo de linhas perpendiculares. Isso ocorre porque é possível tomar apenas três linhas que sejam mutuamente perpendiculares, duas das quais definem o plano e uma terceira que mede a profundidade. Assim, se houvesse alguma outra distância após a terceira, ela seria totalmente desprovida de medida e definição. (MANNING, 1914, p.1. Tradução nossa).

Após o desenvolvimento da álgebra e sua introdução no Ocidente, as possibilidades de operar com múltiplas variáveis intuíam abstrações geométricas difíceis de conciliar e traduzir ao espaço tridimensional euclidiano associado ao mundo natural. Vemos em Diofanto (200 a.C.) expressões como “quadrado-quadrado”, “quadrado-cubo”, e “cubo-cubo” para tentar nomear equações em potências maiores que 3, que eram por vezes evitadas como “irreais”. (MANNING, 1914, p. 2).

A álgebra, aliada à a introdução dos algarismos indo-arábicos na Europa ao fim da idade média, instrumentalizou a superação da concepção naturalista da grandeza numérica, que também auxiliou num próprio descolamento da matemática e suas representações geométricas em direção à abstração: em 1564, Jacomo Castriotto e Giorlamo Maggi publicam o primeiro tratado acerca das projeções paralelas, introduzindo a axonometria dita militar enquanto projeção em oposição à projeção central do Renascimento (Scolari, 2005, p.6); já no século XVII, René Descartes (1596-1650) sistematiza na geometria analítica uma união entre a geometria euclidiana e o mundo das coordenadas numéricas e operações algébricas; Isaac Newton (1643-1727), por sua vez, propõe um novo paradigma científico com a mecânica clássica, incorporando à geometria a dinâmica entre espaço e tempo para explicar o comportamento dos corpos no espaço. E apesar de concepções acerca de uma quarta dimensão, ora física, ora espiritual, existirem na obra de filósofos como Thomas More, Immanuel Kant e Jean D’Alembert (Manning, 1914, pp.3-4), uma aversão ao espaço quadridimensional — operável através da álgebra, mas inconcebível e aparentemente irreconciliável ao mundo físico — permaneceu como tabu até o século XVIII. John Wallis (1616-1703), por exemplo, escreveu acerca da quarta dimensão como um “monstro na natureza, menos possível que uma quimera ou centauro” (MANNING, 1914, p.3).

É apenas no século XIX, que uma nova geração de matemáticos elabora não apenas novas concepções abstratas do espaço geométrico euclidiano, como novas geometrias nas quais os postulados milenares de Euclides não se aplicavam. Dentre estes, o alemão Bernhard Riemann emerge como figura central, e fundamenta muito do que estrutura essa nova concepção moderna da matemática, com novos espaços, novas geometrias, e dissociada das amarras da percepção. Segundo Manning (1914, p.14) “O estudo dessas geometrias nos dá uma visão mais verdadeira da natureza do raciocínio geométrico, e permite nos desvencilhar da intuição.”

É nesse contexto que Charles Howard Hinton desenvolve sua pesquisa de representações do espaço quadridimensional. Neste sentido, as tentativas de representação de certa maneira, colonizam a complexidade inata da realidade à subjetividade humana, e o esforço de Hinton, sua preocupação em se fazer entender, reflete o imaginário de seu tempo diante da ruptura de um paradigma naturalista-euclidiano, no qual a percepção e a subjetividade posicionam-se nos limites da percepção.

A relação entre espaço-tempo, de muito interesse para os físicos, conferiu à geometria quadridimensional um interesse especial — à luz das novas descobertas da física, com a concepção do espaço-tempo de Minkowski e a relatividade de Einstein na primeira década do século XX, uma quarta dimensão ora espacial, ora temporal, arranja conexão com o mundo natural. De certo modo, a quadridimensionalidade assumiu um caráter intersticial entre a grandeza do tempo (atrelada às operações e desenvolvimentos práticos das ciências naturais) e o campo da pura ideação, de tudo aquilo que é por natureza intangível à capacidade humana de observar, sentir e experienciar. Essa natureza dual de interlocução entre euclidiano e não-euclidiano, espaço e tempo influenciará imensamente também as vanguardas da arte.

O Tesserato e a Cor
É importante esclarecer que, dentro do imaginário da época, as intenções iniciais do Suprematismo, com forte caráter místico, e do Neoplasticismo, em parte metafísico, estabelecem diferenças na condução de suas experiências estéticas, advindas de um mesmo arcabouço. As intenções subjacentes às soluções estéticas adotadas de tais produções, se afastam: o Suprematismo de Malevich teve influência de Peter Ouspensky, matemático e esoterista russo ligado à doutrina Rosacruz, mas que viria a publicar seus livros mais influentes depois de seu contato com Malevich. Ouspensky

defende haver por trás do mundo visível um outro mundo, espécie de quarta dimensão, além das três a que os sentidos humanos têm acesso. O suprematismo representaria essa realidade, esse ‘mundo não objetivo’, referido a uma ordem superior de relação entre os fenômenos — espécie de ‘energia espiritual abstrata’ —, que é invisível, mas nem por isso menos real. (Enciclopédia Itaú Cultural)

Entre as intenções subjacentes do Suprematismo e do Neoplasticismo há familiaridade, mas não há coincidência. A sequência de axonométricas produzidas por Van Doesburg interessam em suas possibilidades exploratórias dos meios de representação que incluem ambiguidades, mas que se afastam das questões espirituais ou místicas que rondam a questão do imponderável espaço quadridimensional.

Para chegar a essa produção, é importante ressaltar que Cornelis van Eesteren é uma importante influência para uma busca conciliatória entre os meios da pintura e arquitetura na produção de Van Doesburg, uma ambição discutida inclusive com algum ceticismo entre os neoplásicos (BOIS, 1987). Para Van Doesburg, a cor, que desde 1921 foi investigada como meio de destruição do espaço arquitetônico para estabelecer uma planaridade plástica, em 1923 começa a ser elemento de incremento a uma nova arquitetura, que agora também colabora na criação do espaço neoplástico resumido nos 16 pontos de Van Doesburg no artigo “Em Direção a uma Arquitetura Plástica” (1924). É nesse sentido que é relevante ressaltar o caráter notacional do uso da cor por Van Doesburg:

As paredes, na Maison Particulière — e ocasionalmente áreas de paredes adjacentes a janelas ou cantos — foram pintadas em cores primárias em branco, preto e cinza. Ele utilizou cores — como ele disse ao relembrar seu período com Van Eesteren — para definir altura (vermelho), comprimento (amarelo) e largura (azul). Volume foi designado por cinza, preto e branco. (STRATTEN, 1981. p.116-117)

Nesse sentido, a influência de Hinton é evidente. Na tentaiva de representar o cubo na quarta dimensão Hinton desenvolve um sistema de cores que funciona como notação ou diagrama de transições cromáticas que corresponderiam ao deslocamento das faces do hipercubo (figura 2). Por sua vez, a utilização das cores por Hinton possivelmente tenha uma base inicial na teoria de Riemann, na qual as cores e sua transição seriam uma maneira de representar o deslocamento em superfícies complexas, ou curvas.

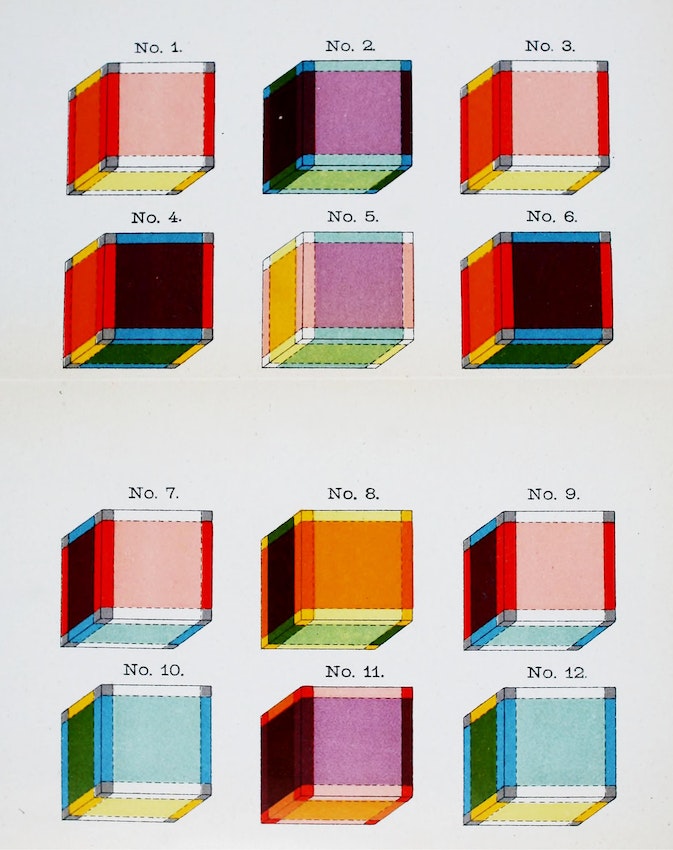
O diagrama de Hinton mostrado na imagem colorida acima, hoje em domínio público, sofre de um certo obscurecimento. Resgatá-lo permite admitir sua influência de forma clara em van Doesburg e, inclusive, em relações mais contemporâneas ao identificar que este diagrama é refeito por Jenny Holzer em 1976, com o título de Twelve views of a 4-D Solid. O artigo de David Joselit (1998, p.58), Voices, Bodies and Spaces: The Art of Jenny Holzer, no qual o trabalho é publicado, faz referência ao importante mergulho de Holzer no universo dos diagramas, mas não demonstra a relação inegável do trabalho de Holzer com o diagrama de Hinton. Como consequência da influência do diagrama de Hinton sobre Jenny Holzer, surge o projeto Painted Room (1978) para a PS1, em que “cada superfície arquitetônica — incluindo tubos e janelas — foi pintada: paredes de amarelo, verde e vermelho; o piso de roxo; o teto de azul” (JOSELIT, 1998. P.58. Tradução nossa), em operação na qual a cor pode ser vista como uma espécie de código, tal qual o faz Van Doesburg no plano representacional em suas Contraconstruções (STRATTEN,1998, p.117).

As Counter-constructions
As contraconstruções se iniciam como desagregações cromáticas —ainda que codificáveis— do objeto de representação (o projeto da Maison Particuliére), exibindo o balanço e interação das cores aplicadas de seus planos e volumes. No entanto, logo assumem um caráter experimental que começa a distanciar-se desse objeto para um discurso gráfico contido na própria representação que também ocorre simultaneamente a um distanciamento de Van Eesteren, logo após a exposição Rosenberg (STRAATEN,1988).

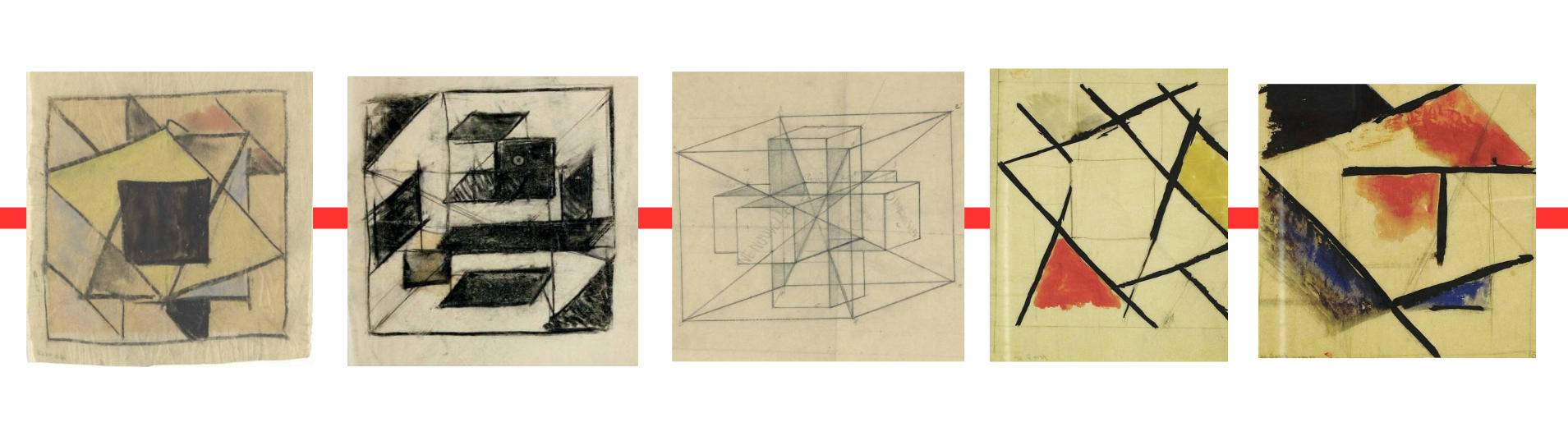
As axonométricas tornam-se um espaço de estudo e testes ora do que é representado, ora da representação em si. Essa dialética desempenha um papel fundamental na percepção da nova espacialidade do século XX, como observada por Bois (EVANS, p.339). Os sucessivos desenhos de Van Doesburg mostram que o equilíbrio e entendimento deste espaço precisavam também ser apreendidos pelo próprio artista, que não hesita em fazer pequenos ajustes na percepção, ordenação e inclusão de alguns de seus elementos compositivos. Certamente influenciado pelos escritos de Hinton, Van Doesburg efetua uma série de estudos a partir do tesserato (figura 6) — ora de precisão técnica, ora rascunhos livres de grande expressividade e uso das cores, que em gradientes parecem emergir e sumir do plano de representação — que se aproximam mais de “impressões” sobre a experiência visual imaginada desses objetos quadridimensionais.

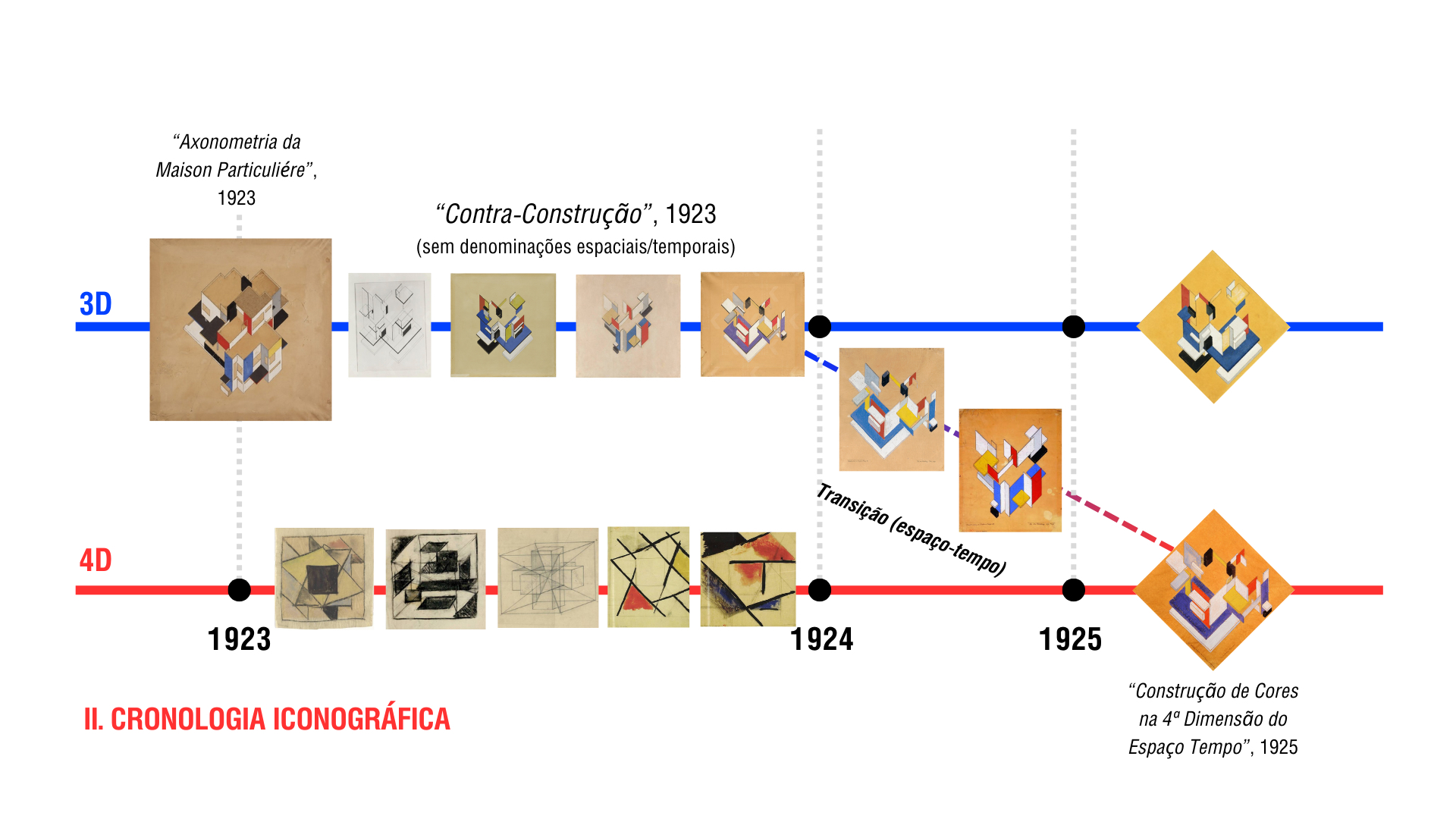
Dentre as Contraconstruções produzidas entre 1923 e 1924, pode-se elencar uma sucessão temporal de obras as quais se destacam pelas denominações específicas que, em conjunto, inferem uma penetração das ideias e investigações contidas nos Estudos Tesseratos. Van Doesburg descola-se do termo “Contraconstrução” para incorporar a intenção do espaço-tempo de Minkowski (figura 7).

Da ambiguidade
Vez ou outra tidas como incorretas ou “risíveis” (EVANS, 1995. p.338.), as axonométricas de Van Doesburg são deliberadamente ambíguas. O dispositivo da projeção axonométrica, utilizado como instrumento de precisão abstrata no campo militar ou da engenharia, requer uma conexão entre as partes do objeto para que este seja passível de leitura correta de suas componentes em verdadeira grandeza (a dimensão real, em escala adequada). No entanto, o procedimento de Van Doesburg consiste em agrupar determinadas partes do objeto em conexão, portanto permitindo tal leitura correta, enquanto insere partes isoladas (paredes, planos) ou grupos de elementos, sem conexão entre si. Próximos, mas desconectados, um plano “flutua” de forma ambígua, sendo impossível determinar sua posição. Neste sentido, e tendo em vista o uso das cores com um parentesco com o diagrama de Hinton, ressaltamos outra camada, de certa forma mensagem cifrada, proposta por van Doesburg; ao repetir a mesma axonométrica renomeando-a com sutis diferenças de cromáticas, datadas em 1923, 1924 e 1925 (hoje em museus diferentes), percebemos que van Doesburg brinca com a representação e assume uma nomenclatura explícita com relação à quarta dimensão.

Palavras Finais
Pretendemos demonstrar que o ato reflexivo investido no fazer artístico de Theo van Doesburg, também imbuído de questões científicas, demonstra uma posição crítica, refletida e atuante, por meio de sua produção gráfico-pictórica. Se sua produção foi mais horizontal, atuando no campo da arquitetura e da arte, e tida como “menor” diante de outros protagonistas de seu tempo, sua influência é sabidamente ampla. Procuramos demonstrar que, um certo “jogo de 7 erros”, proposto por ele entre sutis mudanças de cores e deslocamentos de planos na produção analisada, atesta um controle maior do artista sobre sua produção do que muitas vezes é a ele atribuído. Acreditamos que há ainda mais a desvendar, e que este artigo é, além de um ponto de vista, um ponto de partida.